10452. The essay
At school, Aziz was assigned to write an
essay. The deadline was approaching, and Aziz still hadn’t written anything.
However, he remembered that his friend Barış had already completed
the same assignment last year and decided to use it to his advantage.
Aziz didn’t want the plagiarism detection
system to identify the borrowing, so he came up with a trick: reversing the
words in all the sentences of Barış’s essay. After this, Aziz decided
to calculate the difference between the original sentence and the one he
created.
Barış’s essay consists of t
sentences. Each sentence includes unique words. If the number of words in a
sentence is denoted as n, the original sentence can be represented as
the sequence {1, 2, ..., n}. Aziz’s version of the sentence will then be
represented as the sequence {n, n – 1, ..., 1}.
The difference between the original
sentence and Aziz’s version is calculated as the sum of the absolute
differences between the positions of each word in Barış’s sentence
and the positions of the same word in Aziz’s sentence.
For example, if a sentence consists of
three words and Barış’s sentence is represented as {1, 2, 3}, Aziz’s
sentence will be {3, 2, 1}. In this case, the difference between the sentences
will be:
|1 − 3| +
|2 − 2| + |3 − 1| = 4
Input. The first line contains one integer t (1 ≤
t ≤ 105) – the number of sentences in Barış’s
essay. Each of the following t lines contains one integer ni (1 ≤ ni
≤ 109) – the number of words in the i - th
sentence.
Output. For each sentence, print the difference between
Barış’s and Aziz’s sentences on a separate line.
|
Sample
input |
Sample
output |
|
3 4 3 7 |
8 4 24 |
SOLUTION
mathematics
Algorithm analysis
Let’s find a formula
for solving
the problem based on the number of words n in a sentence.
Let n be an even
number. Let us consider Barış’s and Aziz’s sentences:
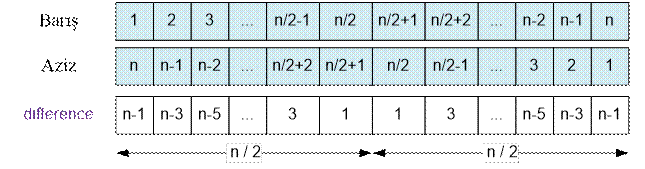
Let’s compute the sum of
the numbers in the “difference” array. Split the numbers in the array into two
equal parts. Find the sum of the numbers from 1 to n – 1 with a step of 2 (this
is an arithmetic progression). There are n / 2 numbers in this
range. Therefore, the sum of all the numbers in the “difference” array is:
![]() =
= ![]()
Let n be an odd
number. Let us consider Barış’s and Aziz’s sentences:
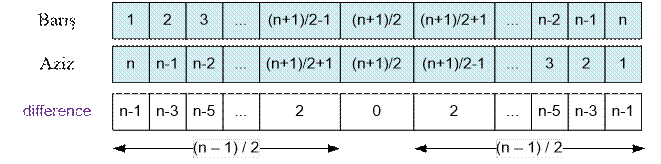
Let’s compute the sum of
the numbers in the “difference” array. Split the numbers in the array into two
equal parts. Find the sum of the numbers from 2 to n – 1 with a step of 2 (this is
an arithmetic progression). There are (n – 1) / 2 numbers in this range.
Therefore, the sum of all the numbers in the “difference” array is:
![]() =
= ![]() =
= ![]()
Example
Let n = 8.
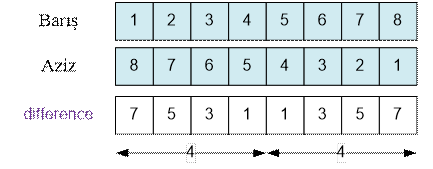
The sum of the numbers in
the “difference” array is 82 / 2 = 32.
Let n = 7.
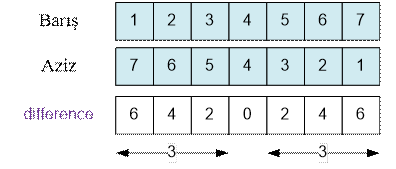
The sum of the numbers in
the “difference” array is (72 – 1) / 2 = 24.
Algorithm implementation
Read the number of test cases tests.
scanf("%d", &tests);
while (tests--)
{
For each value of n, compute and print the result.
scanf("%d", &n);
if (n
% 2 == 0)
res = n * n / 2;
else
res = (n * n - 1) / 2;
printf("%lld\n", res);
}
Python implementation
Read the number of test cases tests.
tests = int(input())
for _ in range(tests):
For each value of n, compute and print the result.
n = int(input())
if n % 2 == 0:
res = n * n // 2
else:
res = (n * n - 1) // 2
print(res)